How to find area

How to find area. The amount of space within a form is measured by its area. In daily life, figuring out a shape’s or surface’s area can be helpful. For instance, you might need to know how much paint to buy to cover a wall or how much grass seed to plant on a lawn.

The fundamentals you need to grasp in order to compute the areas of typical forms like squares and rectangles, triangles, and circles are covered on this page.

Calculating Area Using the Grid Method

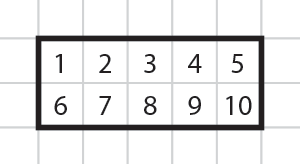
By counting the number of grid squares contained within a form on a scaled grid, you can determine its area.

In this illustration, the rectangle has 10 grid squares inside of it.

We need to be aware of the size that a grid square denotes in order to calculate an area value using the grid method.

Although centimeters are used in this example, the process is the same for any other unit of length or distance. For instance, you might use inches, meters, kilometers, feet, etc.

Calculating a shape’s area using a grid.

Each grid square in this illustration has dimensions of 1 cm in width and 1 cm in height. In other words, a “square centimeter” is the size of each grid cell.

To determine the size of the huge square, count the grid squares inside of it.

The huge square has a surface area of 16 square centimeters due to the presence of 16 little squares.

In mathematics, “square centimeters” is abbreviated as cm2. The 2 denotes a square.

Each grid square measures 1 cm2.

The huge square has a 16 cm2 surface area.

As long as the grid sizes are known, counting squares on a grid to determine area works for all shapes. However, this approach becomes more difficult when forms do not fit the grid precisely or when fractions of grid squares must be counted.

To calculate the area of a shape, use a grid of 1 cm squares.
The square in this illustration does not fit perfectly onto the grid.

By counting grid squares, we can still determine the area.

• 25 entire grid squares are present (shaded in blue).
• 10 half-grid squares (yellow-shaded) — 10 half-squares equal 5 full-grid squares.
• A quarter square, or 0.25 of a square, is also present (it is shaded in green).
• The sum of the whole and fractional squares is: 25 + 5 + 0.25 = 30.25.

The area of this square is consequently 30.25cm2 .

This can also be written as 3014cm2.

Although counting the squares of a form on a grid is a fairly basic approach to learn about area, this method is less useful for determining exact areas of more complex designs because there may be many fractions of grid squares to add.

Depending on the kind of shape you are working with, you can compute area using straightforward formulas.

This page’s remaining content describes and provides examples of how to determine a shape’s area without utilizing a grid system.

Areas of Simple Quadrilaterals:

Squares and Rectangles and Parallelograms

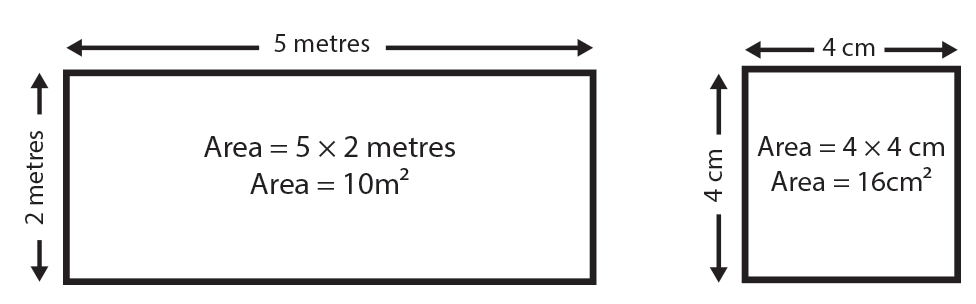
For squares and rectangles, area computations are the most straightforward (and frequently utilized).

Multiply the height and breadth of a rectangle to find its area.

Height x width equals the area of a rectangle.

Since each side of a square is the same length, all that is required to determine the area is to multiply the length of one of the sides by itself. The equivalent expressions for this are length2 and lengthsquared.

It is best practice to measure two sides of a form to see if it truly is a square. For instance, a room’s wall can appear to be square, but upon measurement, it turns out to be a rectangle.

In reality, shapes can frequently be more intricate. Consider the situation when you need to determine the size of a floor in order to order the appropriate quantity of carpet.

A common room floor design can not be a straightforward rectangle or square:

The key in this example, as well as similar instances, is to divide the form into numerous rectangles (or squares). Any of the three options will yield the same outcome, regardless of how the form is divided.

Making two forms and adding their areas together is required for Solutions 1 and 2.

You create a larger shape (A) for solution 3 and deduct the smaller shape (B) from it to find the area

Finding the area of a border, or a form within a shape, is another frequent issue.

In this illustration, a 2 m wide trail circles a field.

Once more, there are various approaches to calculating the area of the path in this illustration.

You may think of the path as four distinct rectangles, calculate each one’s area first, then combine the areas together to get the total.

Calculating the area of the interior rectangle and the entire shape would be quicker. Subtract the area of the internal rectangle from the total, leaving the path area.

Diagram demonstrating how to calculate the size of a shape’s border.
the size of the entire

Diagram demonstrating how to calculate the size of a shape’s border.

The total shape’s area is 16 m x 10 m, or 160 m2.

Because we are aware that the path around the edge is 2 meters wide, we can calculate the central section’s size.

The entire shape is 16 meters wide, and the roadway that runs through it is 4 meters wide (2m on the left of the shape and 2m on the right). 16m – 4m = 12m

Similarly, we can adjust for height: 10m – 2m – 2m = 6m

Therefore, we determined that the central rectangle measures 12 m by 6 m.

Therefore, 12 m x 6 m = 72 m2 is the size of the middle rectangle.

The area of the central rectangle is finally subtracted from the size of the entire form. 160 – 72 = 88m2.

The route has an area of 88m2.

A rectangle is a particular kind of parallelogram since it has four sides and two pairs of them have equal lengths. However, as shown below, the majority of people often picture parallelograms as four-sided structures with angled edges.

figuring out a parallelogram’s surface area.
It’s vital to realize that height does not refer to the length of the vertical (or off vertical) sides, but rather the distance between them when calculating the area of a parallelogram (height width).

As you can see from the diagram, the height is determined by the separation between the shape’s top and bottom sides, not by the length of the side.

Imagine a line that runs between the top and bottom sides at a straight angle. The height is as shown.

How to find area of Triangles

Thinking of a triangle as the bottom half of a square or parallelogram can be helpful.

Half of a square or rectangle is a triangle.

Using the following formula, you can rapidly determine a triangle’s area assuming you know (or can measure) its dimensions:

Triangle’s area is equal to (height x width) / 2.

In other words, you can calculate a triangle’s area in the same manner you would calculate a square or parallelogram’s area. Then, divide your result by 2.

A triangle’s height is expressed as the distance along a right-angled line drawn from its base to its “apex” (highest point).

How to find area of Circles

You must know a circle’s diameter or radius in order to determine its area.

Circle’s diameter and radius

A circle’s diameter is determined by the length of a straight line drawn from one of its sides to the other and passing through its center. The diameter is equal to the radius’s length divided by two.

The distance in a straight line from a circle’s center to its edge is known as its radius. Half of the diameter makes up the radius. (Radius = Diopters Diameter)

The main thing is to measure using a straight line that passes through (for diameter) or finishes at (for radius) the center of the circle. You can measure the diameter or radius at any point around the circle.

In actuality, finding the radius of a circle by measuring the diameter first and dividing it by two is frequently simpler.

To calculate a circle’s area, you must know its radius. The formula is:

Circle area is equal to R2.

This implies:

Pi is a mathematical constant with value 3.142.

The radius of the circle is R.

Radius squared, or R2, is defined as radius radius.